Bayesian VAR and VHAR Models • bvhar

library(bvhar)

etf <- etf_vix[1:55, 1:3]
# Split-------------------------------
h <- 5
etf_eval <- divide_ts(etf, h)
etf_train <- etf_eval$train
etf_test <- etf_eval$test

Bayesian VAR and VHAR

var_bayes() and vhar_bayes() fit BVAR and BVHAR each with various priors.

y: Multivariate time series data. It should be data frame or matrix, which means that every column is numeric. Each column indicates variable, i.e. it sould be wide format.
p or har: VAR lag, or order of VHAR
num_chains: Number of chains
- If OpenMP is enabled, parallel loop will be run.
num_iter: Total number of iterations
num_burn: Number of burn-in
thinning: Thinning
coef_spec: Coefficient prior specification.
- Minneosta prior
  - BVAR: set_bvar()
  - BVHAR: set_bvhar() and set_weight_bvhar()
  - Can induce prior on $\lambda$ using lambda = set_lambda()
- SSVS prior: set_ssvs()
- Horseshoe prior: set_horseshoe()
- NG prior: set_ng()
- DL prior: set_dl()
contem_spec: Contemporaneous prior specification.
cov_spec: Covariance prior specification. Use set_ldlt() for homoskedastic model.
include_mean = TRUE: By default, you include the constant term in the model.
minnesota = c("no", "short", "longrun"): Minnesota-type shrinkage.
verbose = FALSE: Progress bar
num_thread: Number of thread for OpenMP
- Used in parallel multi-chain loop
- This option is valid only when OpenMP in user’s machine.

Stochastic Search Variable Selection (SSVS) Prior

(fit_ssvs <- vhar_bayes(etf_train, num_chains = 1, num_iter = 20, coef_spec = set_ssvs(), contem_spec = set_ssvs(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 1, num_iter = 20, coef_spec = set_ssvs(), 
#>     contem_spec = set_ssvs(), cov_spec = set_ldlt(), include_mean = FALSE, 
#>     minnesota = "longrun")
#> 
#> BVHAR with SSVS prior + SSVS prior
#> Fitted by Gibbs sampling
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 1 chains, and 90 variables
#>      phi[1]    phi[2]   phi[3]   phi[4]   phi[5]    phi[6]  phi[7]   phi[8]
#> 1    0.1246   0.20256  -0.1602  -0.0399  -0.1411  -0.29451   0.665   0.1730
#> 2    0.0856  -0.08727   0.0496  -1.0544  -0.4975  -0.51124   0.604   0.2871
#> 3    0.1175   0.39026  -0.3997  -0.4904  -0.3764   0.06033   1.088   0.8538
#> 4    0.0203   0.03856  -0.0671   0.9171  -0.1068  -0.00241  -0.472  -0.6475
#> 5   -0.0957  -0.00745   0.0141   0.2069  -0.2324  -0.41881   0.135  -0.1364
#> 6    0.1214   0.11141  -0.2002   0.3122   0.0921   0.18845  -0.102   0.0825
#> 7    0.2038   0.04463   0.1374  -0.7403  -0.1705  -0.35122   0.619   1.0751
#> 8    0.0538   0.07403  -0.2746   0.7689  -0.1186   0.24863  -0.447   0.2596
#> 9   -0.0406   0.29739   0.0952  -1.6632  -0.5382  -0.56066   1.892   1.5085
#> 10   0.1080  -0.20321   0.0999  -0.7670  -0.0239  -0.55164   1.051   0.9027
#> # ... with 82 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

autoplot() for the fit (bvharsp object) provides coefficients heatmap. There is type argument, and the default type = "coef" draws the heatmap.

autoplot(fit_ssvs)

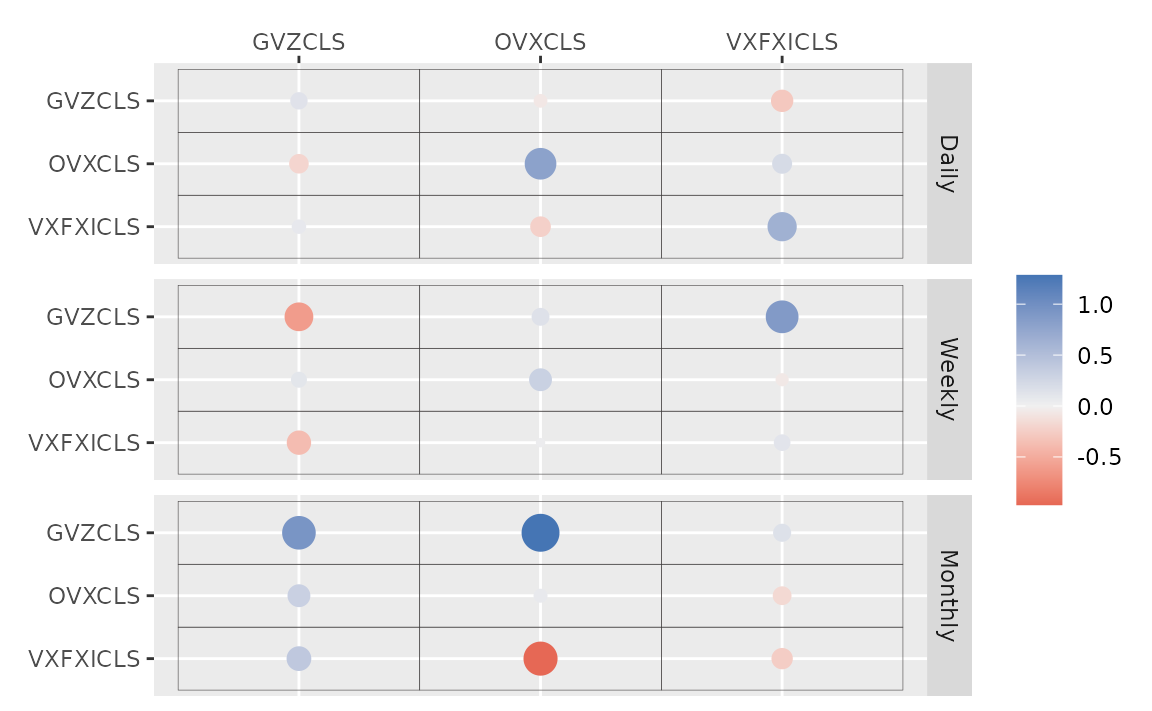
Horseshoe Prior

coef_spec is the initial specification by set_horseshoe(). Others are the same.

(fit_hs <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, coef_spec = set_horseshoe(), contem_spec = set_horseshoe(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, coef_spec = set_horseshoe(), 
#>     contem_spec = set_horseshoe(), cov_spec = set_ldlt(), include_mean = FALSE, 
#>     minnesota = "longrun")
#> 
#> BVHAR with Horseshoe prior + Horseshoe prior
#> Fitted by Gibbs sampling
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 124 variables
#>      phi[1]    phi[2]     phi[3]    phi[4]    phi[5]  phi[6]    phi[7]   phi[8]
#> 1    0.3921  -0.05268  -0.074338  -0.11920   0.00298   1.064   0.01377  -0.0978
#> 2   -0.0734  -0.02555   0.101854   0.24406  -0.01347   0.913   0.00776  -0.1232
#> 3    0.0614  -0.17056  -0.023383   0.35591   0.04498   1.018   0.01497   0.0443
#> 4   -0.0208  -0.21167  -0.082715   0.29275  -0.07747   0.972  -0.03674  -0.0063
#> 5    0.0240  -0.21473  -0.000909   0.20111  -0.00802   1.051   0.04101  -0.0720
#> 6    0.1186  -0.00447   0.021910   0.00658   0.05175   0.965   0.00444  -0.0121
#> 7    0.0783  -0.06972   0.037062   0.02262   0.02518   1.021   0.00290   0.0438
#> 8    0.0969   0.11061  -0.124958   0.06275  -0.01752   0.888   0.02658  -0.0398
#> 9    0.1117  -0.09341   0.125611  -0.02563   0.00331   0.734  -0.05327   0.0348
#> 10   0.1353   0.00398   0.311831   0.00282  -0.03792   0.849  -0.00370  -0.0233
#> # ... with 10 more draws, and 116 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

autoplot(fit_hs)

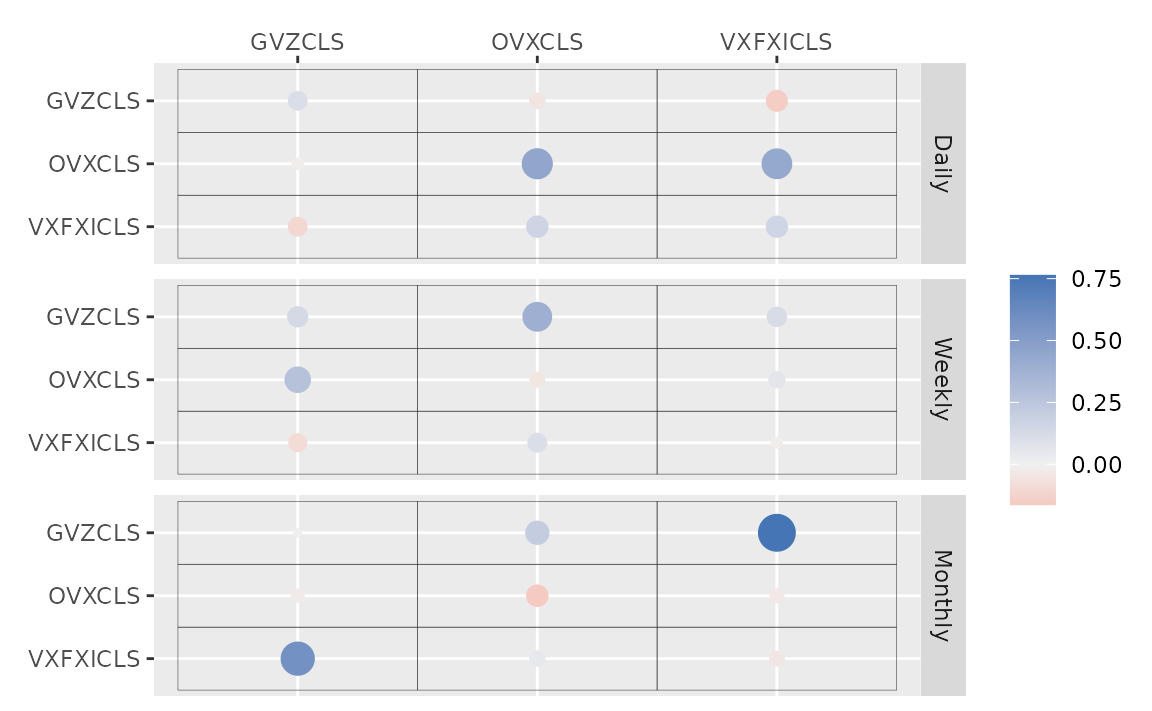
Minnesota Prior

(fit_mn <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, coef_spec = set_bvhar(lambda = set_lambda()), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, coef_spec = set_bvhar(lambda = set_lambda()), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with MN_Hierarchical prior + MN_Hierarchical prior
#> Fitted by Gibbs sampling
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 63 variables
#>     phi[1]   phi[2]   phi[3]   phi[4]   phi[5]  phi[6]   phi[7]   phi[8]
#> 1   0.4138  -0.0515   0.3069  -0.1077   0.4402   1.101  -0.1993  -0.0312
#> 2   0.3537  -0.2305  -0.0559  -0.1199   0.2445   0.917   0.0434   0.1963
#> 3   0.2705  -0.0465   0.0360   0.0420   0.1887   0.874   0.1031  -0.1930
#> 4   0.3118  -0.1969  -0.0404   0.0694   0.0781   0.823   0.1961   0.0728
#> 5   0.4405   0.0575   0.0506   0.0897   0.0893   0.801   0.1058   0.2704
#> 6   0.0848  -0.2301   0.1407   0.0722   0.1061   1.128   0.2398   0.2817
#> 7   0.1809  -0.0362   0.1832   0.1701   0.0527   1.200   0.3462   0.1840
#> 8   0.1078  -0.2035   0.2829   0.3574  -0.0320   1.036   0.1089  -0.0697
#> 9   0.1737  -0.0848   0.3013   0.2573  -0.0513   0.785   0.0675   0.1181
#> 10  0.2752  -0.1289   0.3415  -0.1696   0.0768   0.940  -0.4074  -0.0673
#> # ... with 10 more draws, and 55 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Normal-Gamma prior

(fit_ng <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, coef_spec = set_ng(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, coef_spec = set_ng(), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with NG prior + NG prior
#> Fitted by Metropolis-within-Gibbs
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 97 variables
#>      phi[1]   phi[2]  phi[3]   phi[4]    phi[5]  phi[6]  phi[7]     phi[8]
#> 1   -0.0174  -0.1553   0.144   0.0206  -0.17653   0.105   0.280   7.59e-05
#> 2    0.0609  -0.1648   0.116   0.1234   0.09851   0.355   1.276   1.09e-04
#> 3    0.0601  -0.0281   0.107   0.6836   0.11787   0.329   1.025   1.18e-04
#> 4    0.1942  -0.0493   0.109   0.2376   0.01591  -0.105   0.816   3.30e-03
#> 5   -0.1677  -0.0718   0.124   0.0581   0.02961   0.817   0.393   8.96e-03
#> 6    0.2939  -0.1472   0.112   0.1716   0.16081   0.577   0.690  -7.27e-03
#> 7    0.0951  -0.1081   0.157   0.3563   0.22643   0.512   0.788  -2.35e-02
#> 8    0.0192   0.0252   0.396  -0.0830   0.03402   0.192   0.883  -4.25e-02
#> 9    0.0870  -0.1687   0.224  -0.1649   0.11070   0.317   1.337   1.97e-02
#> 10   0.0754  -0.1531   0.301   0.0207  -0.00271   0.174   0.842  -4.06e-02
#> # ... with 10 more draws, and 89 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Dirichlet-Laplace prior

(fit_dl <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, coef_spec = set_dl(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, coef_spec = set_dl(), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with DL prior + DL prior
#> Fitted by Gibbs sampling
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 91 variables
#>      phi[1]     phi[2]     phi[3]    phi[4]    phi[5]  phi[6]    phi[7]
#> 1    0.1265  -7.42e-04   0.229700  -0.03685   0.00379   1.023   0.09483
#> 2    0.2969  -6.77e-05   0.267984  -0.04788   0.01575   0.892   0.14783
#> 3    0.3211  -2.87e-04   0.061009   0.15042   0.07236   0.929   0.12545
#> 4    0.6038  -2.35e-02   0.055624   0.03182   0.24390   0.890   0.14750
#> 5    0.1682   5.49e-03   0.083656   0.05044   0.32651   0.971   0.28056
#> 6   -0.0813   1.15e-02   0.259276   0.08102   0.02230   0.938  -0.03120
#> 7    0.2164   5.34e-03   0.079894   0.35501   0.04436   0.957  -0.01114
#> 8    0.2066   4.07e-03  -0.003125   0.11486   0.21925   0.979  -0.00265
#> 9    0.0328   1.87e-04  -0.000436  -0.01424   0.03418   0.839  -0.00452
#> 10   0.0639   1.36e-04  -0.003721  -0.00596  -0.00668   0.859  -0.05257
#>        phi[8]
#> 1   -1.58e-01
#> 2   -4.14e-02
#> 3    1.64e-02
#> 4    1.13e-02
#> 5   -1.62e-03
#> 6   -3.18e-03
#> 7    4.21e-03
#> 8    2.38e-04
#> 9   -2.06e-05
#> 10  -1.17e-02
#> # ... with 10 more draws, and 83 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Bayesian visualization

autoplot() also provides Bayesian visualization. type = "trace" gives MCMC trace plot.

autoplot(fit_hs, type = "trace", regex_pars = "tau")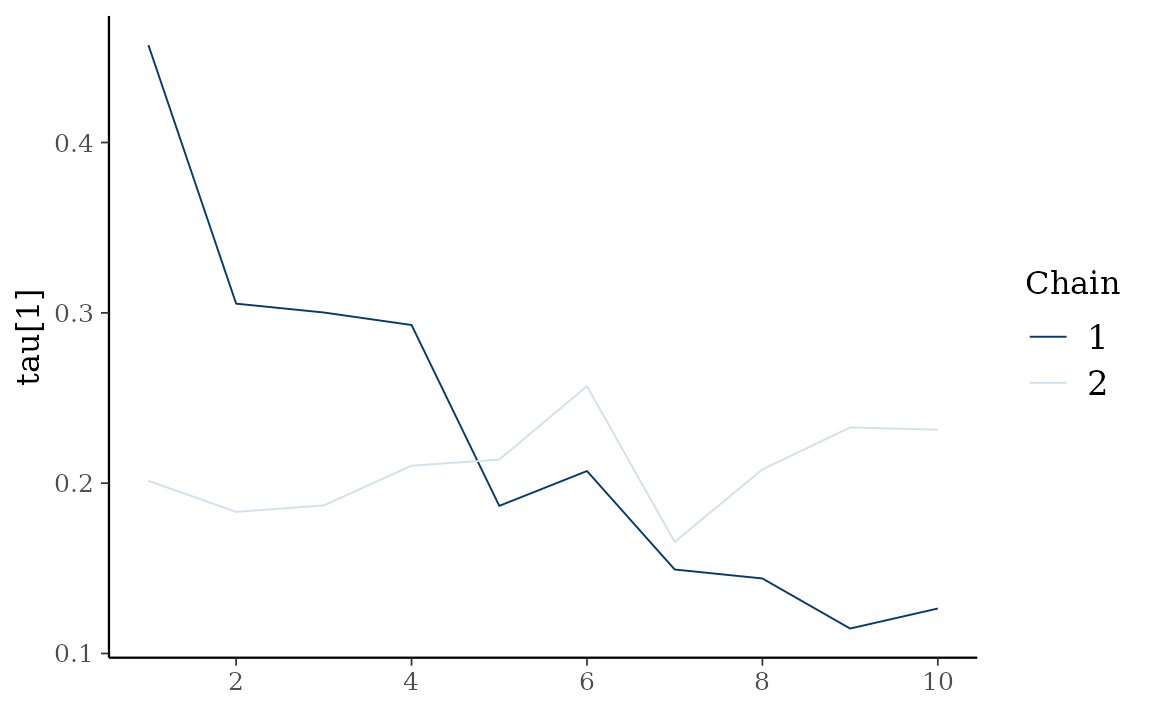

type = "dens" draws MCMC density plot. If specifying additional argument facet_args = list(dir = "v") of bayesplot, you can see plot as the same format with coefficient matrix.

autoplot(fit_hs, type = "dens", regex_pars = "kappa", facet_args = list(dir = "v", nrow = nrow(fit_hs$coefficients)))