Bayesian VAR and VHAR Models • bvhar

library(bvhar)

etf <- etf_vix[1:55, 1:3]
# Split-------------------------------
h <- 5
etf_eval <- divide_ts(etf, h)
etf_train <- etf_eval$train
etf_test <- etf_eval$test

Bayesian VAR and VHAR

var_bayes() and vhar_bayes() fit BVAR and BVHAR each with various priors.

y: Multivariate time series data. It should be data frame or matrix, which means that every column is numeric. Each column indicates variable, i.e. it sould be wide format.
p or har: VAR lag, or order of VHAR
num_chains: Number of chains
- If OpenMP is enabled, parallel loop will be run.
num_iter: Total number of iterations
num_burn: Number of burn-in
thinning: Thinning
bayes_spec: Output of set_ssvs()
- Minneosta prior
  - BVAR: set_bvar()
  - BVHAR: set_bvhar() and set_weight_bvhar()
  - Can induce prior on $\lambda$ using lambda = set_lambda()
- SSVS prior: set_ssvs()
- Horseshoe prior: set_horseshoe()
- NG prior: set_ng()
- DL prior: set_dl()
cov_spec: Covariance prior specification. Use set_ldlt() for homoskedastic model.
include_mean = TRUE: By default, you include the constant term in the model.
minnesota = c("no", "short", "longrun"): Minnesota-type shrinkage.
verbose = FALSE: Progress bar
num_thread: Number of thread for OpenMP
- Used in parallel multi-chain loop
- This option is valid only when OpenMP in user’s machine.

Stochastic Search Variable Selection (SSVS) Prior

(fit_ssvs <- vhar_bayes(etf_train, num_chains = 1, num_iter = 20, bayes_spec = set_ssvs(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 1, num_iter = 20, bayes_spec = set_ssvs(), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with SSVS prior
#> Fitted by Gibbs sampling
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 1 chains, and 90 variables
#>      phi[1]   phi[2]   phi[3]  phi[4]   phi[5]  phi[6]   phi[7]   phi[8]
#> 1    0.0429   0.1032   0.0751  -1.065   0.2814  -0.299   1.9280   1.4308
#> 2    0.3587  -0.2091   0.2117  -0.147   0.2603  -0.212  -0.0805  -0.1194
#> 3   -0.0920  -0.0893   0.1198   0.065  -0.2134  -0.199  -0.0660  -0.0336
#> 4    0.2715  -0.2033   0.1803  -0.724   0.0192  -0.386   1.4648   0.2072
#> 5    0.0187  -0.1021   0.1732  -0.953   0.0856  -0.625   1.3928   0.7355
#> 6    0.1987  -0.1968   0.2466  -0.956   0.1447  -0.558   1.4975   0.4995
#> 7    0.1982  -0.2029   0.0768  -0.831   0.3321  -0.356   1.4978   0.5742
#> 8   -0.1002  -0.3761   0.0268  -0.799   0.1613  -0.499   1.1633  -0.0106
#> 9    0.1921  -0.4328  -0.1678  -0.619   0.0504  -0.333   0.6136   0.0106
#> 10   0.2367  -0.2305  -0.1977  -0.059  -0.1013  -0.316  -0.0623  -0.1687
#> # ... with 82 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

autoplot() for the fit (bvharsp object) provides coefficients heatmap. There is type argument, and the default type = "coef" draws the heatmap.

autoplot(fit_ssvs)

Horseshoe Prior

bayes_spec is the initial specification by set_horseshoe(). Others are the same.

(fit_hs <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_horseshoe(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_horseshoe(), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with Horseshoe prior
#> Fitted by Gibbs sampling
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 124 variables
#>       phi[1]   phi[2]   phi[3]     phi[4]    phi[5]    phi[6]  phi[7]   phi[8]
#> 1   -0.00950  -0.6781   1.0408   0.099660  -0.00867  -0.00638  0.2857   1.2204
#> 2   -0.00484  -0.2053   1.8099  -0.010360   0.21034   0.01308  0.3589   0.1133
#> 3   -0.00853  -0.2376   0.8261   0.000923   0.10468   0.43175  0.4615   0.4400
#> 4   -0.00542  -0.0203   0.0712   0.003396   0.34441   0.17688  0.0340   0.2259
#> 5   -0.00183  -0.0223  -0.0371  -0.002231   2.19899  -0.03177  0.0426   0.0427
#> 6    0.00448  -0.1139   0.0842  -0.000445   2.54582  -0.02232  0.3654   0.1101
#> 7   -0.02708   0.0637   0.6941   0.000747  -0.10755  -0.04615  0.2165   0.1768
#> 8    0.36783  -0.0294  -0.3218   0.000111   1.08201   0.05984  0.4627   0.0699
#> 9   -0.03679  -0.2504  -0.0354   0.000336   0.97651   0.08571  0.2866  -0.1106
#> 10   0.04780  -0.2722  -0.0107   0.000154   0.35662   0.00911  0.0791  -0.0579
#> # ... with 10 more draws, and 116 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

autoplot(fit_hs)

Minnesota Prior

(fit_mn <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_bvhar(lambda = set_lambda()), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_bvhar(lambda = set_lambda()), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with MN_Hierarchical prior
#> Fitted by Gibbs sampling
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 63 variables
#>     phi[1]    phi[2]   phi[3]     phi[4]    phi[5]  phi[6]   phi[7]    phi[8]
#> 1   0.0960  -0.06454   0.0898   0.149039   0.15948   1.286   0.3296   0.17588
#> 2   0.4650  -0.10282  -0.0732   0.359101   0.01651   0.843   0.2547  -0.00466
#> 3   0.4987  -0.35645   0.1462  -0.109077   0.09793   1.257   0.2210   0.01337
#> 4   0.0256  -0.11528   0.1021   0.058250   0.22298   0.909   0.4084   0.13241
#> 5   0.3072  -0.25352   0.2687   0.278917  -0.02073   1.177   0.3303  -0.33796
#> 6   0.1886  -0.16339   0.2272   0.168824   0.02504   0.963   0.0847  -0.30628
#> 7   0.2001  -0.16268   0.0189   0.439802   0.42224   1.013   0.6046   0.05434
#> 8   0.3528  -0.00251   0.3827   0.339542  -0.00989   0.545  -0.3931  -0.44756
#> 9   0.3011  -0.22574  -0.0788  -0.000334   0.22362   0.342   0.4450  -0.12164
#> 10  0.1936  -0.14646   0.0649   0.072367   0.24439   0.686   0.2699  -0.00731
#> # ... with 10 more draws, and 55 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Normal-Gamma prior

(fit_ng <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_ng(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_ng(), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with NG prior
#> Fitted by Metropolis-within-Gibbs
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 97 variables
#>      phi[1]    phi[2]    phi[3]    phi[4]    phi[5]    phi[6]    phi[7]
#> 1    0.0580  -0.04671   0.04265   0.00618   0.06183  -0.00638   0.00719
#> 2   -0.0241  -0.00374   0.08118   0.00090  -0.00117   0.01466   0.00972
#> 3    0.0215  -0.02203   0.08263   0.00032   0.00677   0.03121   0.02480
#> 4    0.0561  -0.09879   0.05613  -0.00130   0.00451   0.19240   0.47467
#> 5    0.2193  -0.05864   0.01103   0.00319   0.14916   0.84141   0.66151
#> 6    0.3382  -0.05972  -0.00619  -0.00962  -0.11705   1.06522   0.22307
#> 7    0.2188  -0.08351  -0.10956   0.03056   0.39904   1.57796   1.88983
#> 8    0.4294  -0.03667   0.11182  -0.03674   0.01666   0.83532  -0.53781
#> 9    0.5016  -0.14089   0.01857  -0.00409   0.02095   0.87700  -0.51530
#> 10   0.1740  -0.05936   0.08638  -0.00131  -0.25196   0.34172   0.29114
#>       phi[8]
#> 1   -0.02518
#> 2   -0.06328
#> 3    0.25823
#> 4   -0.03480
#> 5   -0.08484
#> 6    0.23694
#> 7   -0.05653
#> 8    0.00358
#> 9   -0.00128
#> 10  -0.00449
#> # ... with 10 more draws, and 89 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Dirichlet-Laplace prior

(fit_dl <- vhar_bayes(etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_dl(), cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun"))
#> Call:
#> vhar_bayes(y = etf_train, num_chains = 2, num_iter = 20, bayes_spec = set_dl(), 
#>     cov_spec = set_ldlt(), include_mean = FALSE, minnesota = "longrun")
#> 
#> BVHAR with DL prior
#> Fitted by Gibbs sampling
#> Number of chains: 2
#> Total number of iteration: 20
#> Number of burn-in: 10
#> ====================================================
#> 
#> Parameter Record:
#> # A draws_df: 10 iterations, 2 chains, and 91 variables
#>      phi[1]   phi[2]    phi[3]   phi[4]   phi[5]  phi[6]   phi[7]   phi[8]
#> 1    0.0238  -0.1570   0.13196   1.0106   0.0780   0.156   0.4260   0.2456
#> 2    0.0877  -0.3112   0.01248   0.5559   0.1224   0.836  -0.1151   0.0325
#> 3    0.1909  -0.4841  -0.11611   0.8619   0.0974   0.983   0.3137  -0.0922
#> 4    0.3497  -0.2444   0.26508   0.7810   0.1025   0.648   0.0853   0.0398
#> 5    0.2307  -0.2907   0.23740   0.5146  -0.2804   1.035  -0.1117  -0.0889
#> 6    0.1309  -0.2299  -0.32532  -0.0678   0.5573   1.011  -0.2019  -0.1911
#> 7    0.0915  -0.3254  -0.13914   0.0168   0.2229   0.859  -0.5806  -0.4391
#> 8    0.0854   0.0357   0.00659  -0.0518  -0.3399   0.612  -0.5571  -0.2342
#> 9   -0.0218   0.0390   0.03880   0.2015   0.0897   0.802   0.0890  -0.0269
#> 10   0.1817  -0.1016   0.48692   0.1310  -0.1772   0.914   0.3551  -0.0416
#> # ... with 10 more draws, and 83 more variables
#> # ... hidden reserved variables {'.chain', '.iteration', '.draw'}

Bayesian visualization

autoplot() also provides Bayesian visualization. type = "trace" gives MCMC trace plot.

autoplot(fit_hs, type = "trace", regex_pars = "tau")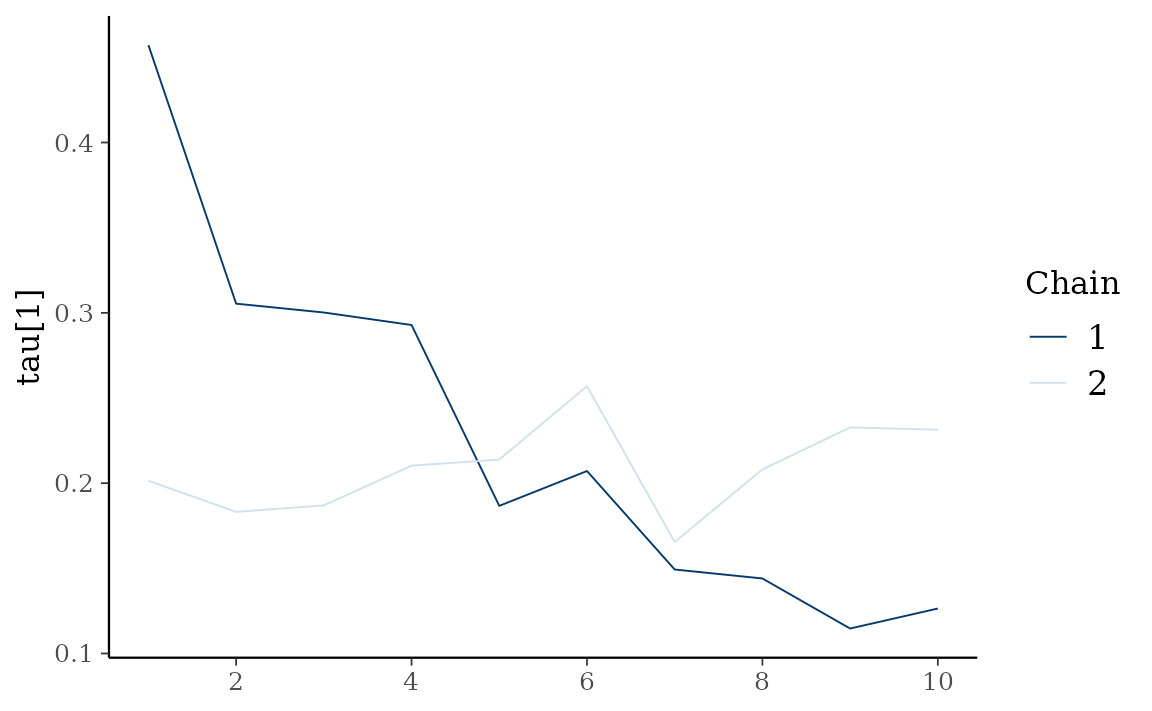

type = "dens" draws MCMC density plot. If specifying additional argument facet_args = list(dir = "v") of bayesplot, you can see plot as the same format with coefficient matrix.

autoplot(fit_hs, type = "dens", regex_pars = "kappa", facet_args = list(dir = "v", nrow = nrow(fit_hs$coefficients)))